The attractive force of a magnet is positively correlated with MF (magnetic field strength) and AS (adsorption surface area). When the WP (working point) of a magnet is near the MBP (maximum energy product), its work capability is maximized, and so is its attractive force. It is important that the adsorbed object is large enough to fully cover the magnetic pole, so that factors such as material, size, and shape of the adsorbed object can be ignored. To determine whether the WP is near the MBP, take Cyl-M (cylindrical magnet) as an example: when H/D ≈ 0.6, the central Pc ≈ 1, indicating maximum attractive force. For instance, with an N35 D10*6 Cyl-M, FEA simulation shows that the attractive force for adsorbing an iron plate is approximately 27N, nearly the maximum for magnets of the same volume, which is 780 times its own weight. Sq-M (square magnet) behaves similarly; when directly adsorbed, its central Pc ≈ 1, achieving maximum attractive force among magnets of the same volume.
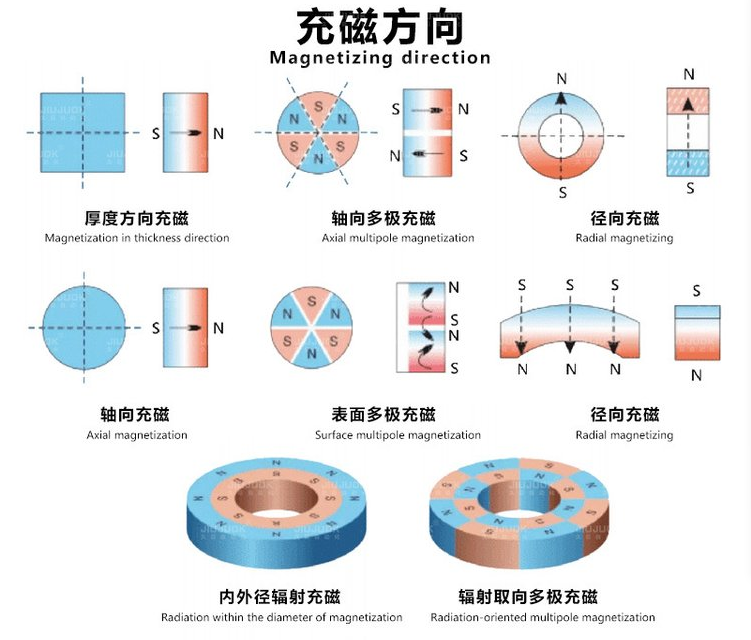
If the magnet is multipole magnetized, the attractive force will be significantly different, with the multipole magnetization providing a much greater attractive force than single-pole magnetization (assuming a small gap between the magnet and the adsorbed object). The reason for such a significant change in attractive force when a magnet of the same volume is multipole magnetized is that while the adsorption surface area S remains unchanged, the magnetic flux density B passing through the adsorbed object increases significantly. This can be seen from the magnetic field line diagram below, where the density of magnetic field lines passing through the iron plate is noticeably higher for the multipole magnetized magnet. Taking the N35 D10*6 magnet as an example, when it is bipolar magnetized, FEA simulation shows that the attractive force for adsorbing an iron plate is approximately 1100 times its own weight. Since the magnet is multipole magnetized, each pole acts like a more elongated magnet, causing the Pc value to change and no longer be calculable based on the overall dimensions. Therefore, the optimal dimension is no longer H/D ≈ 0.6, but rather a flatter magnet, with the specific dimensions depending on the multipole magnetization method and the number of poles.
